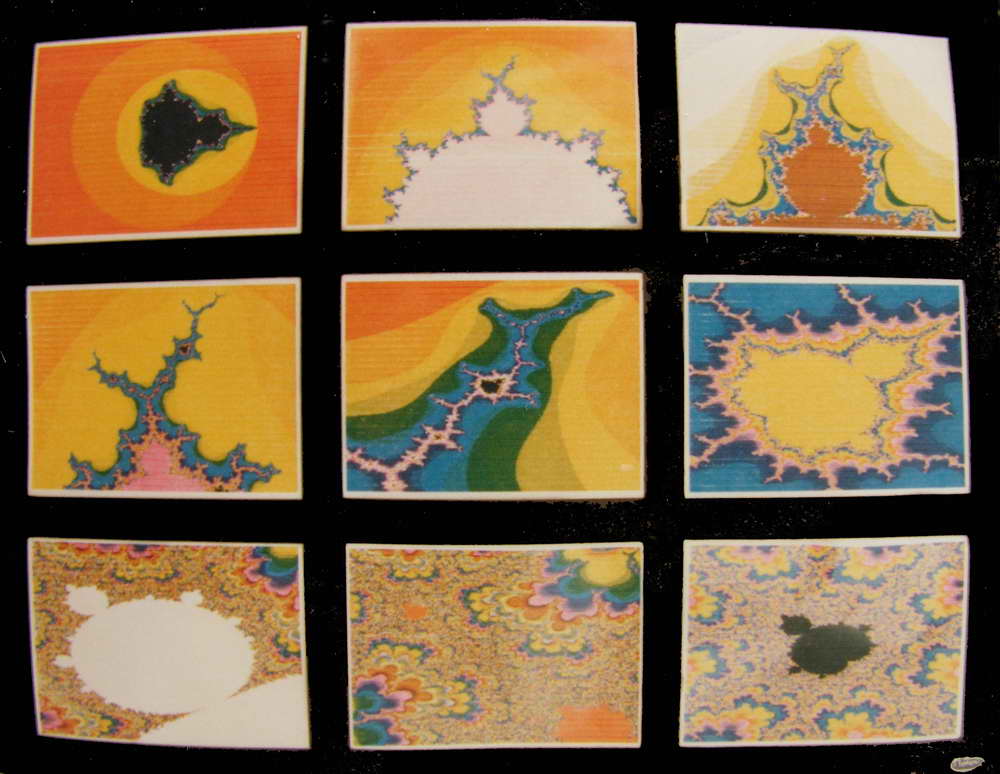
Galerie des Fractals
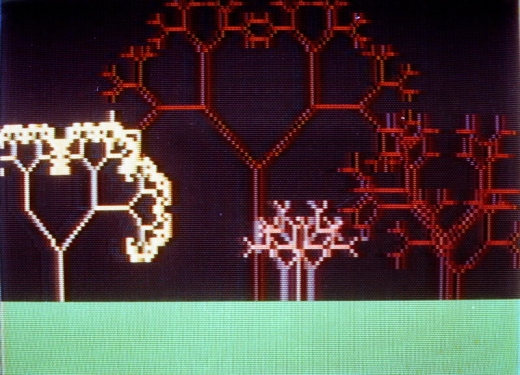
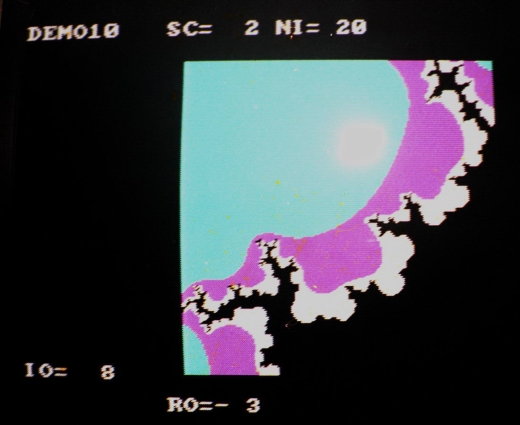
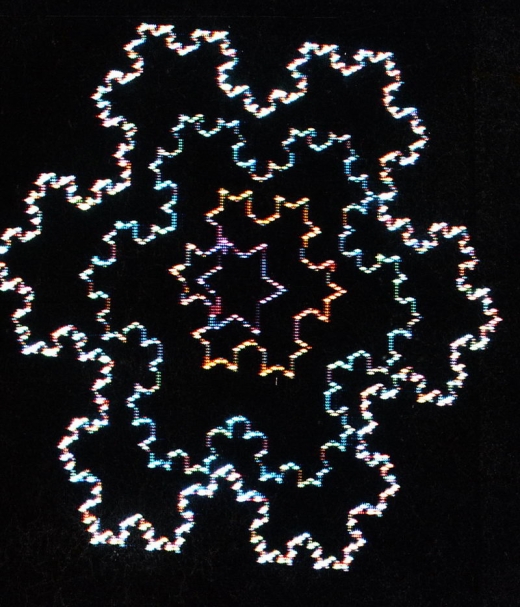

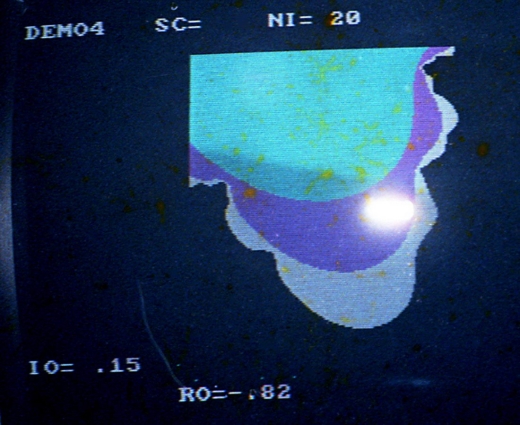
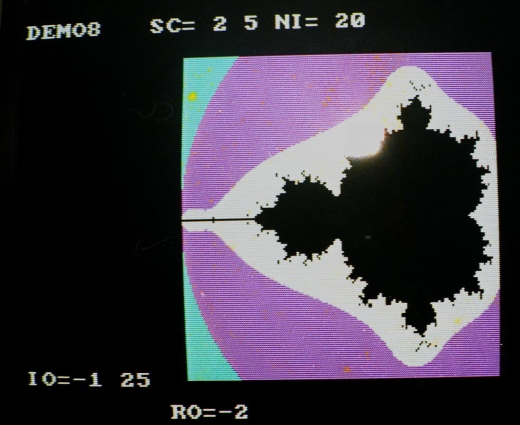
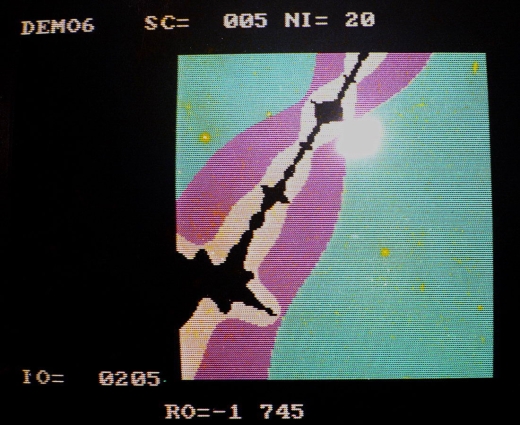



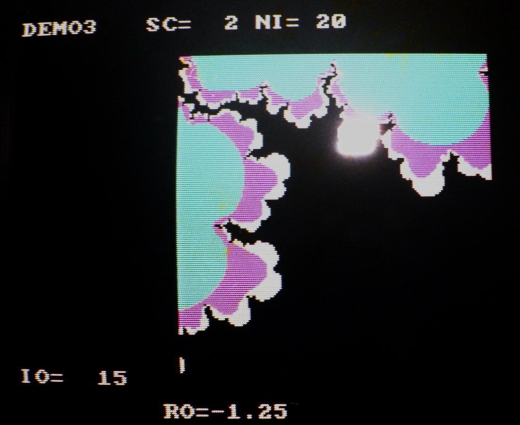


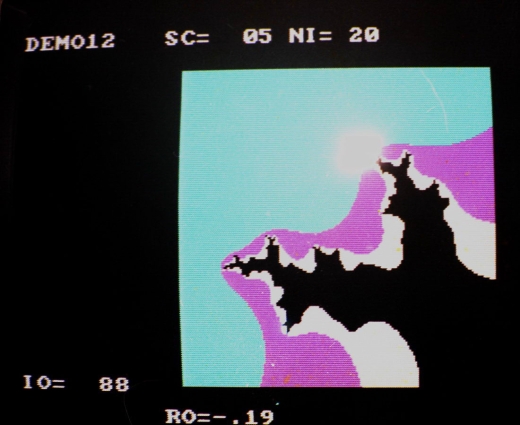
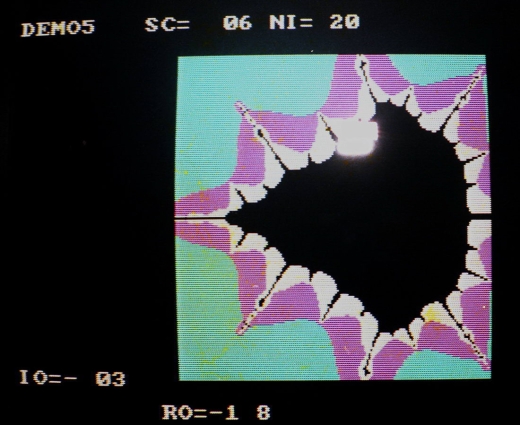

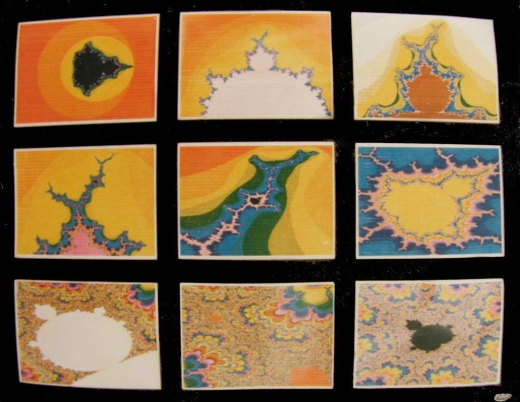
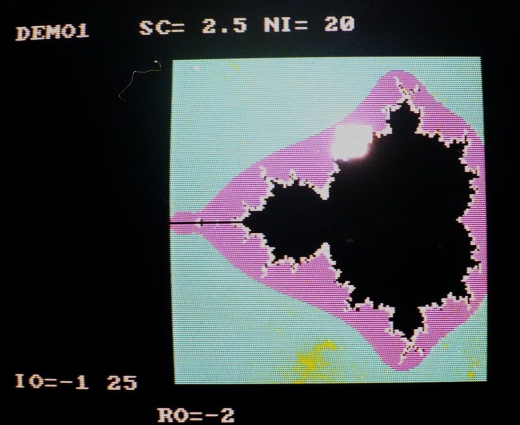


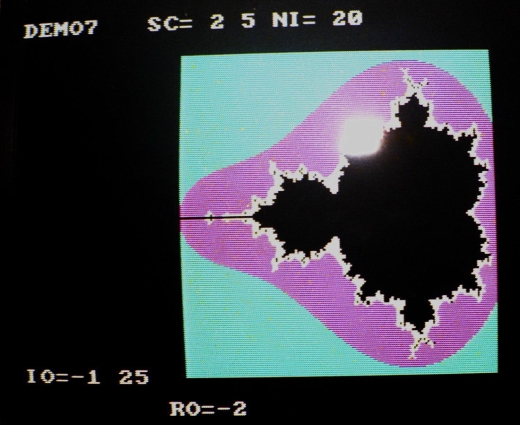

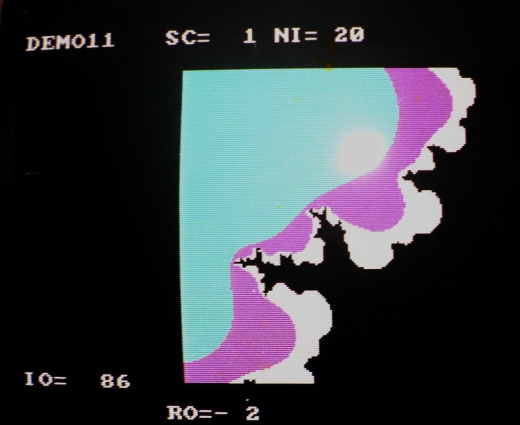



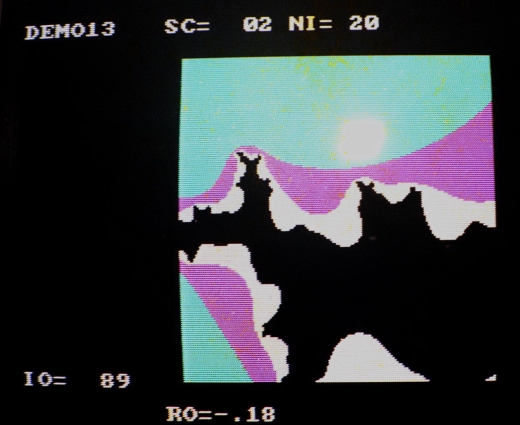




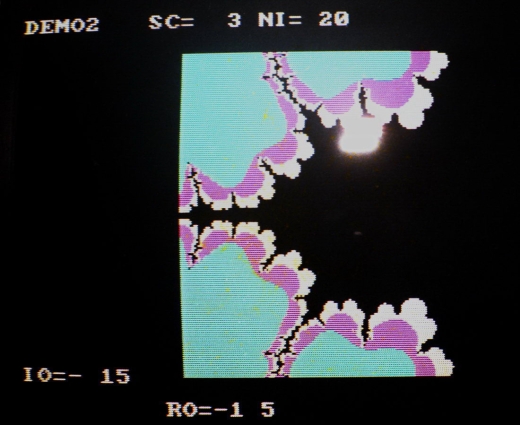

Fractals de Vancouver
J’ai décidé en 1981 de quitter Québec et partir découvrir l’ouest Canadien et en particulier la ville de Vancouver. J’ai poursuivi mes études universitaires à l’University of British Columbia (UBC) et découvert les ordinateurs personnels ce qui m’a donné une nouvelle vision de l’univers et donc de la création artistique.
En 1984, les objets fractales venaient juste d’être découvert par Benoît Mandelbrot et pour les réaliser sur un ordinateur personnel de l’époque (Commodore 64) il fallait écrire des programmes assez complexes et les faire tourner pendant des jours et des nuits entières.
Pour voir un exemple de programme, lisez cet article sur l’ensemble de Mandelbrot.
Pour comprendre les fractales voici un lien vers un article de Wikipedia

Ces fractals ont été montré au public lors de l’expo collective « Grey Point Fractalism », en 1984, à la galerie « Unit Pitt Gallery », Vancouver, Canada
Fractals de Bermuda
En 1987, aux Bermudes j’ai eu accès à un des premiers IBM PC (8086) puis j’ai fait l’acquisition d’un ordinateur personnel super puissant pour l’époque, un Commodore Amiga. Avec ces ordinateurs j’ai enfin pu vraiment explorer le « Mandelbrot Set »…
L’ensemble de Mandelbrot est une fractale définie comme l’ensemble des points c du plan complexe pour lesquels la suite définie par récurrence par :

ne tend pas vers l’infini (en module).
Si nous reformulons cela sans utiliser les nombres complexes, en remplaçant zn par le couple de réels (xn, yn) et c par le couple (a, b), alors nous obtenons :
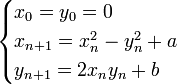
la condition devenant que ni xn, ni yn ne tendent vers l’infini (en valeur absolue).
En language BASIC de l’époque cela donne :
470 PRINT : PRINT « Real origin « ;RO;FNB$(RO); : INPUT IN$ : IF IN$<> » » THEN RO=VAL(IN$)
480 PRINT : PRINT « Imaginary origin « ;IO;FNB$(IO); : INPUT IN$ : IF IN$<> » » THEN IO=VAL(IN$)
490 PRINT : PRINT « Size of the complex plane explored « ;SC;FNB$(SC); : INPUT IN$ : IF IN$<> » » THEN SC=VAL(IN$)
520 PRINT : PRINT « Number of iterations « ;NI%+1;FNB$(NI%); : INPUT IN$ : IF IN$<> » » THEN NI%=VAL(IN$)-1
…
930 IF DP THEN IF MO=1 THEN PRINT : PRINT »Row Col Z Iterations
940 FOR R%=1 TO SW% : FOR I%=1 TO SW%
950 REM————– Search Complex Number Z ————-
960 RC=R%*SP+RO : IC=I%*SP+IO : RZ=0 : IZ=0 : ZZ%=0
970 TZ=RZ : RZ=RZ*RZ-IZ*IZ+RC : IZ=2*TZ*IZ+IC : ZZ%=ZZ%+1 : DZ=SQR(RZ*RZ+IZ*IZ)
980 IF (DZ>2) OR (ZZ%>NI%) GOTO 1000 ELSE GOTO 970
990 REM————– Store zz%, Find min, max, average, « distances » —–
1000 PP%(R%,I%)=ZZ%
1010 IF ZZ%<MI% THEN MI%=ZZ%
1020 IF ZZ%<NI% THEN AV=AV+ZZ% : PO%=PO%+1 : IF ZZ%>MA% THEN MA%=ZZ%
1030 IF MO<>1 GOTO 1080
1040 IF DP<>1 GOTO 1080
1050 IF ZZ%>NI% THEN COLOR 23,0 : ZZ%=20 : GOTO 1070
1060 IF ZZ%<14 THEN COLOR ZZ%,0 ELSE COLOR 15,0
1070 PRINT R%;I%;DZ ; : LOCATE CSRLIN,30 : PRINT STRING$(ZZ%,219)
1080 NEXT I%,R%
1090 IF PO%>0 THEN AV=AV/PO%
1100 IF CS=1 THEN SN=MI% : MN=AV : LN=MA%
1110 IF CS=2 THEN SN=MI%+(AV-MI%)*2/3 : MN=AV+(MA%-AV)/3 : LN=MA%
1120 IF CS=3 THEN SN=AV : MN=AV+(MA%-AV)/2 : LN=MA%
Pour consulter le programme complet (en BASIC PC 1985), téléchargez ce fichier : MANDSET.TXT
Regardez ce zoom vertigineux dans l’ensemble de Mandelbrot réalisé de nos jours sur un ordinateur puissant. Si un IBM PC 8086 de 1985 devait calculer cette image en BASIC, cela prendrait des années…
Art Digital
Depuis 2022, les fractals produit à l’époque sont disponibles comme œuvres digitales sur mon espace OpenSea.io
Les œuvres sont toutes enregistrées dans une chaîne de blocs (blockchain Ethereum) ce qui garantie leur authenticité grâce à des Jetons non fongible (NFT).
Vous pouvez donc enfin acheter ces très rares Fractals datant de 1984.
https://opensea.io/olivier_moreau